Geoid

Äquipotentialfläche des Schwerefeldes der Erde, welche den mittleren Meeresspiegel bestmöglich approximiert. Betrachtet man das Meerwasser als frei bewegliche Masse, welche nur der aus Gravitation und Zentrifugalkraft zusammengesetzten Schwerkraft unterworfen ist, so bildet sich die Oberfläche der Ozeane nach Erreichen des Gleichgewichtszustandes als Niveaufläche des Schwerepotentials aus. Diesen idealisierten Meeresspiegel kann man sich (etwa durch ein System kommunizierender Röhren) unter den Kontinenten fortgesetzt denken, so daß eine geschlossene Fläche entsteht, die das Geoid veranschaulicht. Mit dem auf einen Raumpunkt mit dem Ortsvektor x bezogenen Schwerepotential W(x) lautet die Gleichung des Geoids: W(x)=W_o= const.

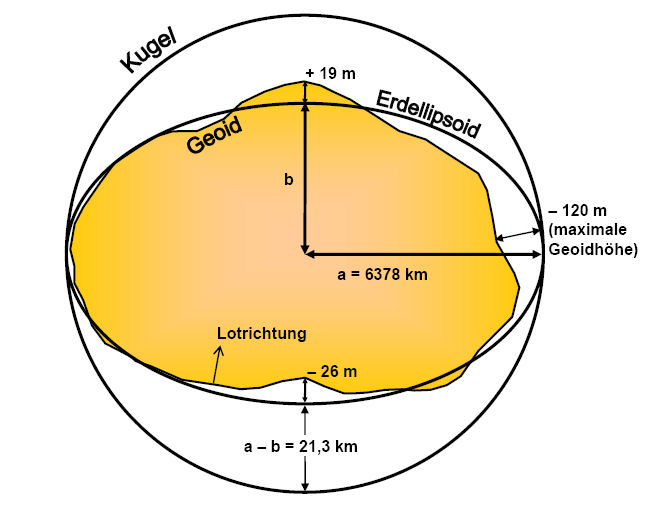Form der Erde

Geoid im Vergleich zu Kugel und Erdellipsoid

Alle Punkte auf der Erde besitzen ein sog. Potential, das sich aus der Kombination von Gravitationskraft und Zentrifugalkraft der Erde ergibt. Diejenige 3D-Äquipotentialfläche, die der Oberfläche der "ruhenden" Weltmeere entspricht und sich unter den Kontinenten fortsetzt, wird als Geoid bezeichnet.

Quelle: BMI

Das Geoid als eine teilweise im Innern der Erdmasse verlaufende Fläche ist stetig und stetig differenzierbar, besitzt jedoch Unstetigkeiten in der Flächenkrümmung an allen Unstetigkeitsstellen der Massendichte und ist somit keine analytische Fläche. Aufgrund der unregelmäßigen Verteilung der Massendichte im Erdkörper kann das Geoid nicht durch eine algebraische Flächengleichung beschrieben werden, sondern muß mit terrestrischen oder satellitengestützen Methoden der Geodäsie bestimmt werden. Das Geoid ist Bezugsfläche für die orthometrischen Höhen.

Ein auf der Datengrundlage der Satelliten LAGEOS, GRACE und GOCE und von Oberflächendaten, Fluggravimetrie und Satelliten-Altimetrie erstelltes Geoid-Modell erhielt den Beinamen "Potsdamer Schwerekartoffel".

Weitere Informationen:

Das Potsdamer Geoid. Beitrag von Peter Schwintzer und Christoph Reigber, GFZ (Sterne und Weltraum 8/2002)
Das Schwerefeld der Erde. Beitrag von Christoph Reigber und Peter Schwintzer, GFZ (Physik in unserer Zeit 5/2003)